Download

Anexact but Rigorous: The Territorial Delimitations of Sejima and Nishizawa

Miguel Paredes Maldonado


The introduction of the notion of the anexact as it pertains to the generation of architectural form can be considered one of the most valuable contributions to the discourse of our discipline in the last two decades. It has principally been associated with the work of Greg Lynn, who redeployed the term ‘anexact’ for an architectural audience as a framework for the description of complex three-dimensional forms enabled by and conceived via digital technologies.^[01] The importance of this contribution cannot be understated, however this paper will endeavour to extend the range of anexact thinking by exploring the two-dimensional space of architectural drawing, which still constitutes the main field of operations for design practices. It will do so by looking at practices—such as those of Kazuyo Sejima and Ryue Nishizawa—that do not explicitly engage with digital modelling mediums.^[02]

The anexact was originally defined by Edmund Husserl in his 1936 paper ‘The origin of geometry’ and famously scrutinized at length by Jacques Derrida in his introduction to Husserl’s text. For Derrida, the anexact is manifested through vague morphological types, which give rise to a form of descriptive science based on the observation of objects being perceived as a whole.^[03] Using the work of Husserl and Derrida as a conceptual scaffold, Lynn formulated a distinction between exact, inexact and anexact geometries that is particularly relevant in the context of architecture. According to Lynn, exact geometries are those that can be reduced to fixed mathematical systems, therefore allowing precise reproduction. On the contrary, inexact geometries lack the necessary rigor and precision to allow for measurement. As a consequence of this, our ability to reproduce them is limited. Finally, anexact geometries refer to constructions that, while being irreducible to specific points and dimensions, are nevertheless rigorous insofar they can be described with precision. In other words, anexact geometries can indeed be measured and therefore faithfully reproduced. Where the exact deals with geometries that are reproducible due to their idealised, abstract nature (for example circles, squares, etc.)  Lynn considers the anexact to be a form of geometry that can be described and measured with precision, but nevertheless deviates from idealised form.^[04] The key aspect of the anexact is the fact that its geometrical construction takes place within the ‘real space’ of what is perceived; it is not an abstract construct. In this sense, we can picture the anexact as the outcome of specific forces affecting a given material field, intimately linking anexact geometry to the domain of matter.^[05]

Further to this distinction, Lynn argued that architecture has historically tended to rely on repeatable, universally translatable geometries. In doing so, particularities and differences could be framed as variations within a universal set of proportions, which could in turn be expressed as a series of types.^[06] As a consequence, proportional bodies become conflated with geometric exactitude, and by extension with the notion of the exact advanced by Husserl. Such an idealised approach to proportion, harmony and internal balance tends to cancel out individual differences. Within such framework individual objects would tend to converge towards an average configuration, embodied by the type from which such configurations would—at least theoretically—originate. In contrast to this model, the anexact highlights the expressive capabilities of difference; it alleviates the tendency to smooth out difference.^[07]

By way of an example, in what follows I will discuss the work of Sejima and Nishizawa as an architecture of anextactitude. Upon consideration of their joint body of work it becomes evident that plan drawings constitute their single most prevalent design instrument.^[08] From an operational perspective, the projection of geometry onto the ground plane seems to be the fundamental method for the generation of systems of spatial organisation. The following paragraphs will elaborate on how these plan drawings are structured, and how this projection constitutes an anexact practice in Sejima and Nishizawa’s work. Further to this, I will describe how they mobilise this anexact practice to deploy architectural operations based on the delimitation and the foundation of territories.

The drawings that illustrate this contribution correspond to the plans of a number of projects selected from the body of work of Sejima and Nishizawa. At first glance, it is clear that they all share a common trait: the outline of the plan projections is based on simple, primarily curvilinear geometrical shapes. Further observation reveals that the contour lines that articulate the outline of each plan seem to describe figures which are ‘almost’ circular or ‘almost’ oval, but are never in exact correspondence to conventionally established geometrical primitives; contrary to circles or ovals, the aforementioned figures cannot be described by means of simple mathematical formulae. In the case of plan drawings composed by a set of figures (or by a single, more complex figure) it is useful for us to zoom in and focus our attention on isolated sectors of their contour lines. In doing so, we will notice that these sectors are either ‘almost’ circular arcs or ‘almost’ straight stretches, which nevertheless resist being classified into exact categories such as ‘circular arc’ or ‘straight line’. If we zoom even further into these contour lines we can start working with observation criteria that have a strong resonance with those used in differential calculus. Such an observation would entail considering the contour lines at stake as entities comprised by a multiplicity of very small fragments. Moreover, and rather than being analysed in the context of the totality of the contour line, each fragment would be examined only with regards to its degree of continuity with contiguous fragments. This leads us to a scenario based on a continuous deployment of form, which would in turn be developed in a differential (and therefore local) manner.


01. Ryue Nishizawa. Access Canopy, Kumamoto Train Station, 2007. Scanned output from drawing apparatus.


02. Drawing Ryue Nishizawa’s Access Canopy with the Anexact-but-rigorous drawing machine. Video Still.

In the case of the drawings that constitute the core subject of this article we can observe that all differential sectors contributing towards the composition of the outlines of each plan are, in principle, individually measurable fragments. This results in a multiplicity of circular arcs and straight lines that gradually assembles itself in front of us, establishing local relationships of tangency between contiguous sectors. This continuous operation does, in turn, construct the architectural contour line that defines and delimitates each plan. Such contour can thus be described as a ‘line of lines’, a multiplicity that our gaze apprehends as a single, continuous trace. Further scrutiny of the differential contours articulating Sejima and Nishizawa’s plan drawings reveals an internal organisation that deviates from the established canon of abstract Euclidean geometry by way of non-compliance with two of its most critical axiomatic postulates: metric measure (the understanding that distances between all components of a given spatial set are defined) and parallelism (the existence of parallel lines within the aforementioned spatial set).^[09] With regards to the former, each individual fragment in the contour does indeed cover an individually measurable distance. However, the geometry of the contour as a whole does not emerge from an overall metric scheme, but rather—as elaborated further in the next paragraphs—develops in a self-referential manner. In other words, there is additive metric development but not an overall metric system in place. This also holds true with regards to parallelism, which is only apparently enforced as a geometric construction system in the development of Sejima and Nishizawa’s plan drawings. Once the topographical undulations of the territories where each drawing is grounded are taken into account, lines that are parallel form the perspective of a planar projection are, in fact, not so when considered in three-dimensional space: There is more than one potential parallel to any given sector, which in the absence of an overarching axial system can only be drawn in reference to the sector that preceded it. In that sense, it can be argued that their anexact mode of development makes Sejima and Nishizawa’s drawings gravitate towards the category of the non-Euclidean.^[10] This conceptual framework can be used as the basis for an examination of each specific plan drawing, and when seen collectively this recurrent interrogation of geometric (an)exactitude highlights a number of variations within the geometric strategies deployed by Sejima and Nishizawa. This piece will consider two different scales of enquiry: a micro scale concerned with the gradual development of the plan outline at the local level, and a macro scale that focuses on the formal comparison of the closed figures.

At the micro scale it is possible to identify at least three different generative processes within the collection of projects presented in this paper. For instance, the outline of the multipurpose complex in Onishi is grounded on a series of points acting as the centres of multiple circular arcs. Each arc is tangent to at least one other arc, thus constructing a continuous figure, completely devoid of corners, that defines the boundary of the building plan in a single gesture. A different methodology can be found in the design for the access to the Kumamoto train station. In this particular case, the shape of the roof canopy is inscribed within a dense orthogonal grid, which provides a local space of coordinates that is used as a reference for the location of the outline points. A third approach can be found in the design of the Amsterdam Lumière Pavilion, based on the self-referential generation of the outline: each differential fragment is described exclusively according to a tangency with its preceding fragment. In all three cases the relevant strategies for the development of outlines are manifested as sets of auxiliary structures, scaffolding of sorts, allowing for the construction of a principal trace.


03. Kazuyo Sejima, Multifunctional complex, Onishi, 2003. Scanned output from drawing apparatus. Drawing by Miguel Paredes.


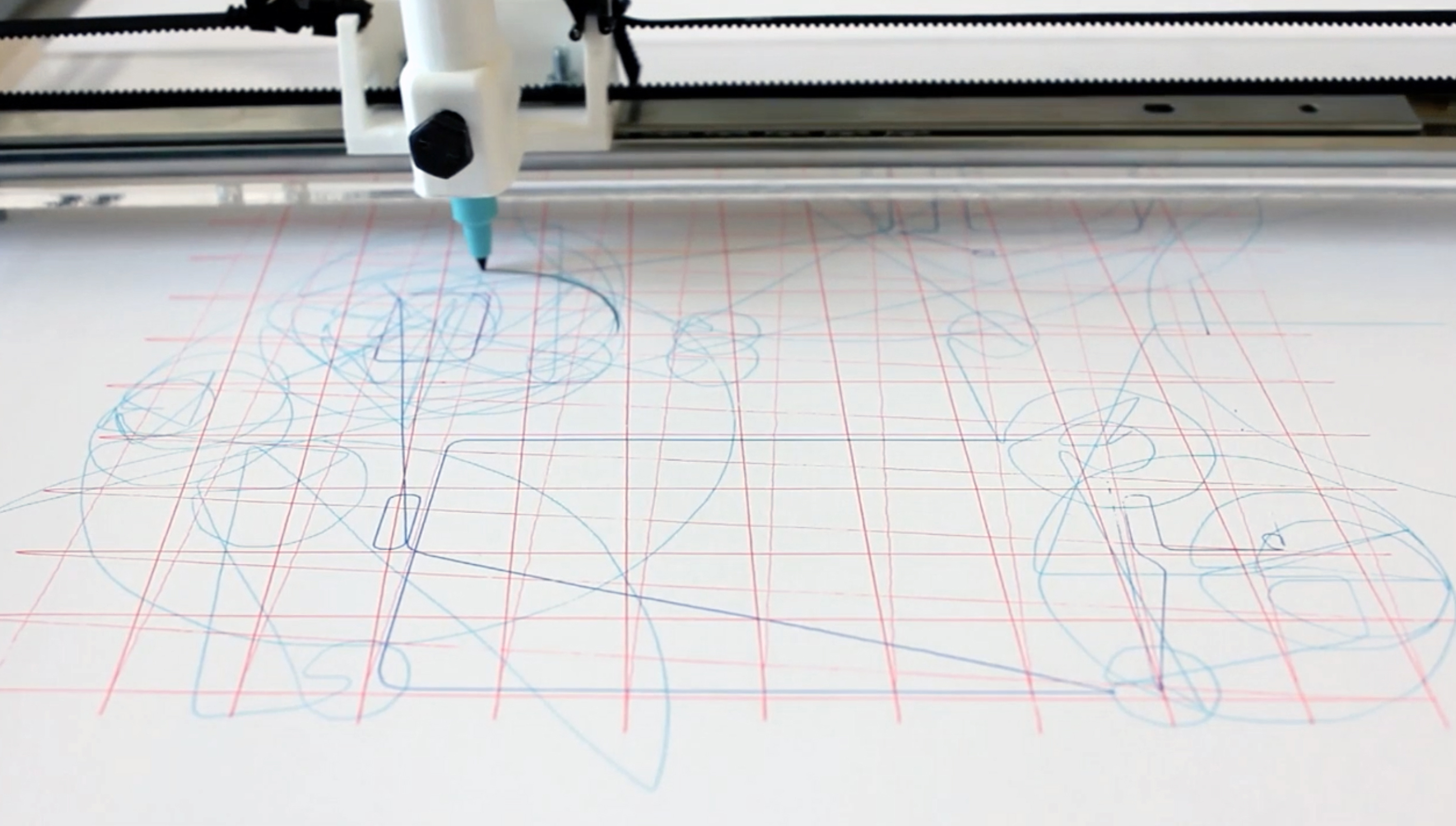
04. Drawing Kazuyo Sejima’s Multifunctional complex with the Anexact-but-rigorous drawing machine. Video still.

At this scale, it is possible to put forward a simple taxonomy of three distinct formal families. The first family would refer to figures that approximate the form of the circle as an essential geometrical entity, with almost no noticeable accentuations in their outlines. A second family would encompass all instances of formal development based on alternating convex and concave sectors while enclosing a central region. The result of this operation would bear some resemblance with the abstracted forms of leaves and flowers. Finally, a third family would entail a distribution within a field populated with objects, which would in turn establish relationships of proximity or remoteness with one another, either opening up spatial regions or wrapping themselves around them as a capturing device of sorts. It should be noted that the individual shape of any of the aforementioned objects could, in turn, correspond to either the first or the second formal family. It is worth noting here that the micro and the macro sets of generative strategies are not isolated, but rather exist in dialogue with one another, allowing for productive, trans-scalar friction. This condition, in turn, facilitates the emergence of a very broad range of potential design configurations using a relatively low number of variable parameters.

Further scrutiny of the taxonomy of micro-scale generative strategies will promptly reveal a strong resonance between the ‘outline’ we are referring to and Paul Klee’s notion of the ‘moving point’. For Klee, any linear element would emerge from a point that jumps over itself and radiates a dimensional space.^[11] Interestingly, Klee also understood the development of lines as a purely dimensional operation, insofar as all their constituent properties (length, angle, length of radius and focal distance) are quantities subject to measurement.^[12] Our observations of Sejima and Nishizawa’s drawings reveal a strikingly similar approach. Their plan outlines emerge from a multiplicity of measured lines, each element being tangent to both the preceding and succeeding fragment to ensure full continuity. Sejima and Nishizawa’s lines are gradually wrapped around themselves, giving rise to closed figures and describing a non-orthogonal space, developed on the horizontal plane and comprising two domains: the inside and the outside. This mode of development is also attuned to Wassily Kandinsky’s reflections on both the parameters that govern linear traces and the spatial effects that such traces create. Kandinsky argued that the particular shape of any given line is the material outcome of forces of tension and direction, but also that, upon drawing a closed line, we are actually constituting a plane.^[13] Thus, as reflected in the drawings of Sejima and Nishizawa, an endless multiplicity of potential planes can be constructed by continuously combining curved lines towards the generation of a closed figure.

An important insight here is that both Klee’s and Kandinsky’s conceptions of pictorial space are fundamentally anexact, insofar as they describe a domain that is simultaneously measurable and non-Euclidean. Moreover, we can argue that this anexactitude emerges in exactly the same terms as in Sejima and Nishizawa’s plan drawings, i.e. through the undermining of the axioms of metric measure and parallelism. Beyond this conceptual resonance, reflecting further on Klee’s and Kandinsky’s insights is useful to gain a better understanding of the intent of Sejima and Nishizawa’s drawing methodology. In both cases, the key operation is the differential union of segments, grounded on an understanding of the resulting accumulative line as a form of delimitating trace. As in Kandinsky’s curvaceous drawings, the ‘almost’ geometrical shapes produced by Sejima and Nishizawa emerge from processes of local negotiation between internal and external tensions. In their particular case, this ‘local negotiation’ occurs in the connection between individual linear segments, where internal tensions respond to criteria of topological continuity and geometrical tangency, and external tensions comprise solicitations arising from the territorial domains in which their plans are deployed. A number of variations on this central theme of the anexact, accumulative outline point toward additional nuances in the drawings of Sejima and Nishizawa, For example, the variable thickening of lines suggests a way of intensifying the trace (thus qualifying the outline alongside its full length), while the intertwining of two outlines (articulating local moments of intensification, or the development of rhythmic patterns) as constituent elements of two corresponding planar domains creates series of nested interior and exterior spaces. Although there is no evidence to suggest any form of direct historical or intellectual reference in Sejima and Nishizawa’s drawings, it should be noted that the aforementioned operations had already been outlined with striking exactitude in Kandinsky’s written work, dating back to 1926.^[14]

If exact geometries converge towards abstract, idealised models, we can argue that the anexact opens itself up to the kind of relational scenarios described above. The geometrical model of the anexact also resonates strongly with that of the ‘nomad science’ described by Deleuze and Guattari, and illustrated through the character of the journeyman in the context of the construction of Gothic cathedrals. Rather than producing a set of representational scale drawings, the journeyman would proceed by directly delimitating boundary regions as full-scale traces drawn on the ground, thus determining the internal and external outlines of the building on site.^[15] In tune with previous distinctions between the exact and the anexact, the work of the journeyman is non-Euclidean, albeit not necessarily less rigorous than that emerging from Euclidean geometries assembled through modern scale drawing conventions. Nonetheless, a key difference between these two modes of operation is that, by directly negotiating the nuances of the site as a full-scale, non-neutral surface, the journeyman has no use for the stasis of idealised geometrical models. On the contrary, he proceeds dynamically by occupying the site with the marking-off of limiting traces, which define themselves gradually and continuously over time.

In turn, the action of gradually tracing the outlines of potential built boundaries has the effect of organising the surface of the site in a territorial manner, acting on and extracting from its particular set of available mediums. Paraphrasing again the work of Deleuze and Guattari, these territorial actions displace the components of the aforementioned mediums away from the directional and towards the dimensional.^[16]

The building outlines of Sejima and Nishizawa, marked off as traces in plan drawings, are rhythmic, dimensional actions that construct territorial regions by delimitating their insides and outsides. The geometrical description of the outline with regards to its gradual deployment results in the emergence of a reproducible boundary, which is nevertheless inscribed on the surface of its specific material field of action. Much like Kandinsky’s figures, Sejima and Nishizawa put forward a protogeometry—simultaneously anexact and rigorous—that rejects pure Euclidean figures in favour of transformations of their essential shapes. This is precisely the kind of geometries that Deleuze and Guatari referred to as being diffuse and emerging from conditions that are somewhat attached to corporeal, material aspects. ^[17]

The curved lines of Sejima and Nishizawa are ‘rounded’ but not ‘circular’. In tune with Deleuze and Guattari’s description of the anexact, they are diffuse, problematized elements but not essences. Rather than relying on the abstract operation of juxtaposing a grid over an idealised ground plane, the plans of Sejima and Nishizawa seem to emerge through the foundation of habitational territories, balancing the fluid tensions of human movement with the more permanent solicitations of the contexts where they are deployed.

Coda #1

The redrawn plans of Sejima and Nishizawa’s buildings illustrating this piece attempt to reconstruct the geometric operations through which their boundary outlines were originally inscribed on their respective territorial surfaces. In so doing, these (re)drawings emphasise their own anexact-but-rigorous construction, referring explicitly to the generative strategies that were presented in this text. However, it is imperative to acknowledge the limited ability of the static drawing format to fully convey the gradual unfolding of actions over time that constitutes a fundamental aspect of anexact-but-rigorous processes. This reflection takes us back to Deleuze and Guattari’s journeyman, for it is clear that the builder’s dynamic, accumulative occupation of the site is precisely the kind of anexact-but-rigorous endeavour that this piece is attempting to capture.

Therefore, the video put forward as an accompaniment to this text acts an extension of the redrawing process that began with the text, resituating the passing of time at the core of the protogeometrical actions of Sejima and Nishizawa. The agent of this time-based operation is no other than a robotic impersonator of the ancient journeyman: a custom-built CNC drawing machine connected to the author’s desktop computer.

The drawing machine does not simply reproduce the plans that were previously redrawn—a regular desktop printer could be used for that—but rather enacts a process of gradually setting up the layout of built forms over time. In so doing, it deploys a series of auxiliary structures, some of which describe the particularities of the physical territory in which it operates. Its drawing head moves across this increasingly charged landscape of the drawing, tracing the geometric operations that will form the scaffold for the designed intervention, which appears gradually through the accumulative overlap of multiple drawing layers. This reveals much more than the outlines of the final built form: all the operations that need to be undertaken for those outlines to emerge are physically traced. By re-enacting this habitational territory as a gradual, accumulative occupation, the drawing machine becomes an updated version of the Gothic journeyman, rendering visible the full set of discrete instructions that it is meant to carry out, this time in the form of CNC code.^[18]


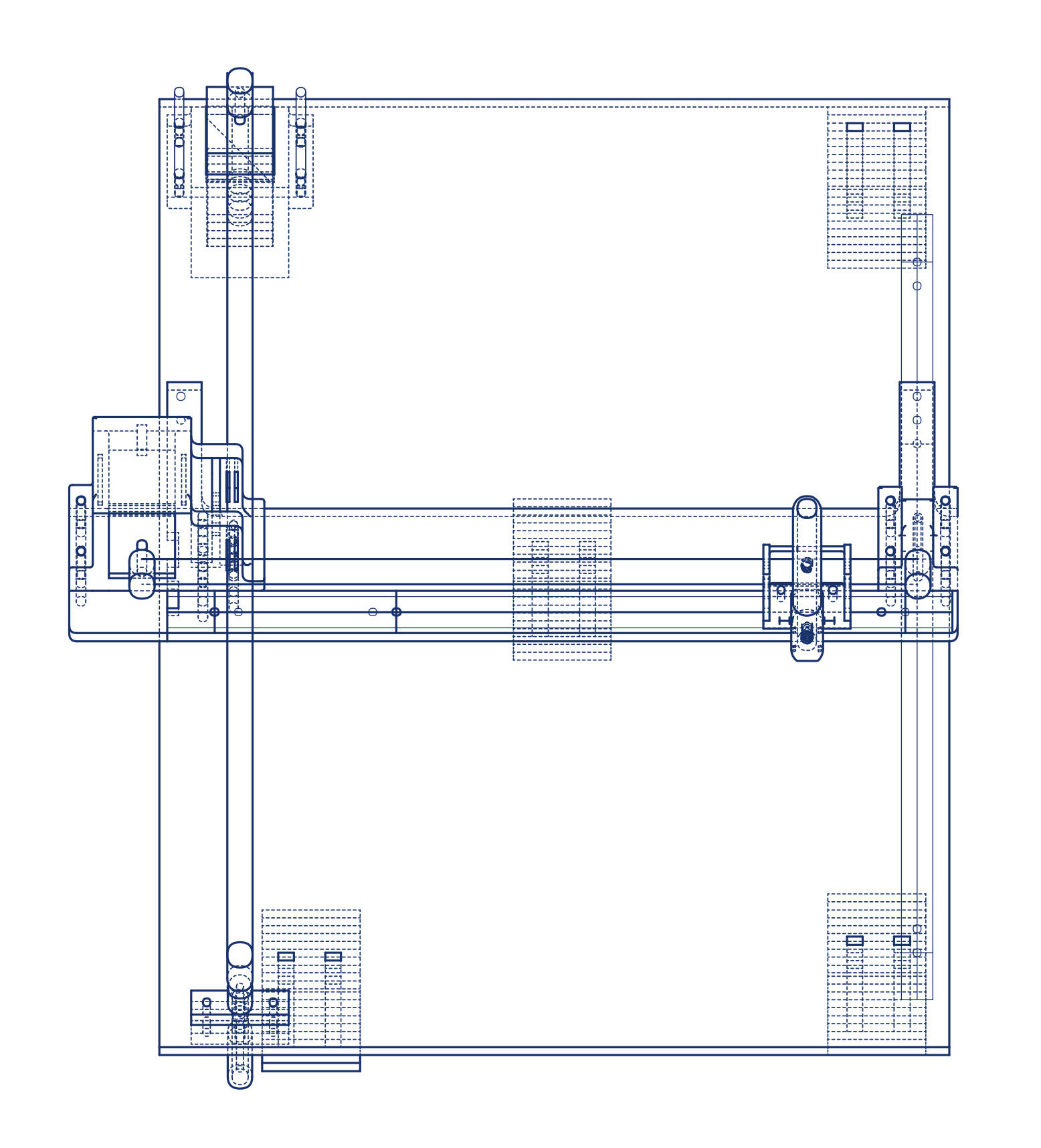
05. Anexact-but-rigorous drawing machine.

In that sense, the drawing machine can be considered as a spatial device, performing both as a descriptor of surfaces (insofar as it provides a system for describing the occupation of the three-dimensional surface of the sites at stake, for which the plotting bed acts like a flattened proxy) and an installing apparatus (insofar as it literally enacts the installation of an architectural geometry onto a proxy space of its own). Thus, the drawings emerging from these acts of machinic installation—documented in the accompanying video—should be regarded as partial registrations of architectural forms emerging through inhabitation, with the anexact form appearing as the gradual accumulation of potentially infinite traces being inscribed on the surface of the landscape.

It is worth adding an additional reflection on the hybridisation of analogue and digital modes of production that is afforded by the drawing machine. As any other digital fabrication tool, this device turns discrete (and therefore instantaneous) digital code into an analogue (and therefore continuous) stream of instructions. By both forcing physical materialisation and rendering the digital-analogue flow of information visible, the machine installs itself halfway between the abstraction of Euclidean geometry that governs the original digital model and its non-Euclidean, anexact process of territorial emergence, which can only be faithfully re-enacted as an accumulative action over time.

Coda #2

Is there scope for turning this analytical apparatus (composed of assembled textual and robotic operations) into a projective tool? The final exhibits in the associated video document ongoing attempts to further interrogate the protocols and potentials of this anexact mode of machinic installation. Firstly, a number of anchor points are digitally fixed, almost as pins in a physical drawing. Potential enclosures for this anchored landscape are then calculated, however subsequent outlining operations are carried out only on the physical surface of the paper. Once again, the drawing machine slowly renders the territorial emergence of these imaginary delimitations visible.


Published 12th March, 2018.


Notes
[01]   Lynn, G. 1993. ‘Multiplicitous and in-Organic Bodies’, Architectural Design, Vol. 63, pp.30–37.

[02]    It is interesting to note that, in the context of the distinction between Euclidean and non-Euclidean design methodologies that often grounds broader discussions on the impact of digital technologies in architecture, the work of Sejima and Nishizawa is typically decidedly aligned with the Euclidean. See, for example: Radman, A. 2014. ‘Architecture of Immanence’, in  Architecture &, Dorian Wiszniewski, Ella Chmielewska, and Tahl Kaminer (eds.), p.4.

[03]    Derrida, J. 1978. Introduction to the Origin of Geometry. Stony Brook, NY: Nicolas Hays. The anexactthus appears as an assemblage of both the aforementioned morphologically vague types and the methods that are used to describe them. It is therefore both a characteristic of those types—as objects—and a particular mode of operation. The goal of this piece is to interrogate the latter.

[04]    Lynn, G. 1993. ‘Multiplicitous and in-Organic Bodies’, pp.30–37.

[05]    Reiser, J. and Umemoto, N. 2006. Atlas of Novel Tectonics. New York: Princeton Architectural Press, pp. 145–146.

[06]    Lynn, G. 1993. ‘Multiplicitous and in-Organic Bodies’, pp.30–37.

[07]    Lynn, G. 1993. ‘Multiplicitous and in-Organic Bodies’, pp.30–37.

[08]    It should be noted that the body of work I am referring to here encompasses that of the individual practices of Sejima and Nishizawa, as well as that of their joint practice, SANAA.

[09]    Cache, B. 2011. ‘Plea for Euclid’, in Projectiles. London: Architectural Association, pp. 31–59. Up until the 18th Century Euclidean geometry was the only available geometrical system for the abstract description of space. It emerged as a systematic synthesis of formerly isolated theorems developed by earlier Greek and Egyptian mathematicians, compiled by Euclid in his book Elements. It is primarily based on five axiomatic postulates, which originally extended into a series of formal proofs and eventually evolved into a comprehensive, saturated, self-consistent system of 21 axioms compiled by David Hilbert in Grundlagen der Geometrie (1899).

[10]    In ‘Plea for Euclid’ Cache notes that: “Non-Euclidean geometries can be generated either the by the negation or the suppression of each of these 21 axioms.”

[11]    Deleuze, G. and Guattari, F. 1987. A Thousand Plateaus: Capitalism and Schizophrenia, trans. by Brian Massumi. Minneapolis: University of Minnesota Press, p.312.  This quote reflects Deleuze and Guattari’s reading of Klee’s On Modern Art (Klee, P. 1948. On Modern Art. London: Faber and Faber).

[12]    Klee, P. 1948. On Modern Art. London: Faber and Faber, p.21.

[13]    Kandinsky, W. 1979. Point and Line to Plane. New York: Dover, p.58. The former would constitute an internal characteristic of straight lines, whereas the latter would articulate external force fields modelling the shape of curved lines

[14]    Kandinsky, W. 1979. Point and Line to Plane, pp.136–140.

[15]    “The ground-level plane of the Gothic journeyman is opposed to the metric plane of the architect, which is on paper and off site.” Deleuze, G. and Guattari, F. 1987. A Thousand Plateaus, p.368.

[16]    “The territory is in fact an act that affects milieus and rhythms, that ‘territorializes’ them... The territory is not primary in relation to the qualitative mark; it is the mark that makes the territory. Functions in a territory are not primary; they presuppose a territory-producing expressiveness. In this sense, the territory and the functions performed within it are products of territorialization…The marking of a territory is dimensional, but it is not a meter, it is a rhythm.” Deleuze, G. and Guattari, F. 1987. A Thousand Plateaus, p.314.

[17]    “Husserl speaks of a protogeometry that addresses vague, in other words vagabond or nomadic, morphological essences. These essences are distinct from sensible things, as well as from ideal, royal, or imperial essences. Protogeometry, the science dealing with them, is itself vague, in the etymological sense of ‘vagabond’: it is neither inexact like sensible things nor exact like ideal essences, but anexact yet rigorous (‘essentially and not accidentally inexact’). The circle is an organic, ideal, fixed essence, but roundness is a vague and fluent essence, distinct both from the circle and things that are round (a vase, a wheel, the sun). A theorematic figure is a fixed essence, but its transformations, distortions, ablations, and augmentations, all of its variations, form problematic figures that are vague yet rigorous, ‘lens-shaped’, ‘umbelliform’, or ‘indented’. It could be said that vague essences extract from things a determination that is more than thinghood (choseite), which is that of corporeality (corporeite).” Deleuze, G. and Guattari, F. 1987. A Thousand Plateaus, p.367.

[18]    “Designing with code unravels new horizons both in the world of design and in the world of production. Taking advantage of the architecture of the Computer Numerical Machine (CNC) machine—these machines read code, not drawings or 3D models—an immediate relationship between design and machine can be established.” Oosterhuis, K. 2017. ‘Emotive Embodiments’, in Critical and Clinical Cartographies, ed. by Andrej Radman and Heidi Sohn. Edinburgh: Edinburgh University Press, pp.168–183.

Figures